What is a Capacitor?
A capacitor is a
passive circuit element that has the ability to store electrical energy in the form
of an electrostatic electric field.
A typical capacitor consists of two conducting plates that are separated by an insulating material (or dielectric material) as shown in figure-1. The capacitor stores electrical energy in the form of electrostatic charge and it can be connected to an electric circuit so that this stored energy can be made to flow into the circuit to perform a useful function. The property of the capacitor by which it stores energy is called capacitance. We will learn about capacitance in the upcoming sections of this article.
Capacitors play an important role in AC as well as DC
circuits. In many circuits like radio and TV circuits, capacitors are used to introduce
a desired capacitance. It must know that an ideal (or pure) capacitor does not
dissipate energy but stores it which can be released at a later time.
The metal surfaces of the capacitor are known as the plates of the capacitor and the
insulating material separating the capacitor plates is called the dielectric. The most commonly used
dielectric materials in practical capacitors are air, mica, waxed paper,
ceramics, and electrolytes.
Working of Capacitor
In this section, we will learn that how a capacitor stores
the electric charge when connected to a source of electrical energy.
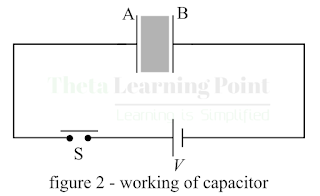
Consider a parallel plate capacitor having two plates A and B separated by a dielectric material and connected to a battery
through a switch S as shown in
figure-2.
The following steps explain the working of the capacitor-
Step 1 – With the switch S open as shown in the figure-2. There is no potential difference between the plates of the capacitor, and hence they are neutral.
Step 2 – When the switch S is closed as shown in figure-3. Plate A will be at a positive potential and plate B will be at a negative potential. The result is that an electric field directed from plate A to B will appear inside the capacitor. This electric field will polarize the dielectric placed between the plates.
The polarization of the dielectric will be such that the end of the dielectric near the positive plate will be negatively charged and the end near the negative plate will be positively charged. In this way, the external energy supplied by the battery is utilized to polarize the dielectric material between the plates of the capacitor. Thus, it is to be noted that the capacitor stores the electrical energy in the form of electrostatic charge in the dielectric material, and is said to be charged.
Step 3 – The process of polarization of the dielectric continues till the potential difference across capacitor plates becomes equal to battery voltage V. When the capacitor is charged to battery voltage V. The polarization of the dielectric stops.
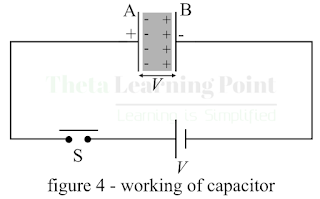
Step 4 – If now the switch S is opened as shown in figure-4. The capacitor will retain the charges. Therefore, the capacitor which was neutral at the start now has charges stored in it.
These four steps show how a capacitor stores electric
charge.
What is Capacitance?
The ability of a capacitor to store electrical energy in the
form of electrostatic charge is called the capacitance
of the capacitor. Capacitance is usually represented by the symbol C.
Experimentally, it has been observed that charge (q) stored in a capacitor is directly
proportional to the potential difference (v)
across it, i.e.
Where C is a constant called the capacitance of the capacitor.
Equation (1) may also be written as,
`\"Capacitance",C=q/v" "…(2)`
Hence, the capacitance of a capacitor may
be defined as under-
The
ratio of the charge on either plate to the voltage (or potential difference) across
the plates of a capacitor is called the capacitance
of the capacitor.
Unit of Capacitance
From equation (2), it can be seen that
`\"Unit of Capacitance"="Coulomb"/"Volt"`
Thus, the unit of capacitance is coulomb per volt (C/V). But, the
practical unit of capacitance is Farad
(F). It is named in the honor of Michael
Faraday.
1 Farad (F) = 1 C/V
Thus, the unit of capacitance, Farad, may
be defined as under:
The
capacitance of a capacitor is said to be of 1 Farad if a charge of 1 coulomb
accumulates on each plate when a voltage of 1 volt is applied across the plates
of the capacitor.
Although, the Farad is a very large unit
of capacitance. Practical capacitors have capacitances of the order of
microfarad (µF), nano farad (nF), or picofarad (pF). Where,
`\1" μF"=1×10^(-6)" F"`
`\1" nF"=1×10^(-9)" F"`
`\1" pF"=1×10^(-12)" F"`
Factors Affecting Capacitance
The capacitance of a capacitor depends
upon the physical dimensions of the capacitors. For example, for the parallel
plate capacitor, the capacitance is given by,
`\C=(ϵA)/d=(ϵ_0 ϵ_r A)/d" "…(3)`
Where A is the surface area of each plate, d is the distance between the plates, and ε
is the permittivity of the dielectric material between the plates.
Hence, from equation (3), it is clear
that the capacitance of a capacitance depends upon the following three factors:
(1).
Surface area of the plates – The larger the surface of the
capacitor plates, the greater the capacitance.
(2).
Distance between the plates – The small the
distance between the plates of the capacitor, the greater the capacitance.
(3).
Permittivity of the dielectric material – The higher the
permittivity of the material, the greater the capacitance.
Types of Capacitors
Capacitors can be classified into different
types depending on different factors of classification. Some common
classifications of capacitors are given below.
Classification
1 – Based on variation in capacitance, capacitors are classified as:
- Fixed
Capacitors – These capacitors have a constant value
of capacitance.
- Variable
Capacitors – The capacitance value of the variable
capacitor can be changed.
Classification
2 – Based on polarization, capacitors are classified as:
- Polarized
Capacitors – These capacitors have a specified
polarity. Thus, these are used in DC circuits only.
- Non-Polarized
Capacitors – These capacitors do not have a
definite polarity. Thus, they can also be used in AC circuits.
Classification
3 – Depending on the dielectric material used, capacitors can be classified
into the following types:
- Ceramic Capacitors
- Film Capacitors
- Electrolytic Capacitors
- Paper Capacitors
- Air Capacitors
- Mica Capacitors, etc.
Current-Voltage Relationship in Capacitor
We can obtain the current-voltage relation of the capacitor by integrating the equation (1) on both sides, i.e.
`\(dq)/dt=C (dv)/dt`
Since,
`\i=(dq)/dt`
Therefore,
`\i=C (dv)/dt" "…(4)`
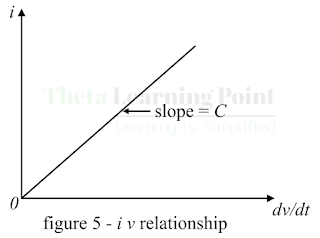
Equation (4) is the current-voltage
relationship of a capacitor. Figure-5 represents the current-voltage relationship for a capacitor whose
capacitance is independent of voltage. A capacitor that satisfies equation (4)
is known as a linear capacitor. When
the plot of the current-voltage relationship of a capacitor is not a straight
line, it is called a non-linear
capacitor.
`\∫i dt=C∫(dv)/dt dt`
`\⟹v(t)=1/C ∫_(-∞)^t i(τ)dτ" "…(5)`
Or,
`\v(t)=1/C ∫_(t_0)^t i(τ)dτ+v(t_0)" "…(6)`
Where,
`\v(t_0)=(q(t_0))/C`
It is the voltage across the capacitor at
time t0. From equation
(6), it is clear that the voltage across a capacitor depends upon the past
history of the capacitor current. Hence, the capacitor has memory.
Energy Stored in a Capacitor
When an electrical voltage is applied
across a capacitor, the capacitor stores energy supplied by the source in the
form of an electrostatic field. On discharging the capacitor, the stored energy is
released back into the circuit.
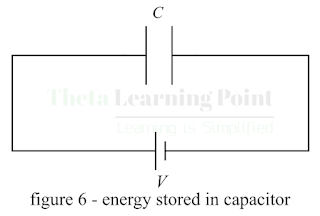
Now, let us calculate the energy stored
in the capacitor. Consider a capacitor of C
Farad being charged from a dc source of V
volts as shown in figure-6.
Assume at any instant of the charging period,
the electric charge on the capacitor is equal to q coulombs and the voltage across the plates of the capacitor is v volts. Then, the capacitance of the
capacitor is given by,
`\C=q/v" "…(7)`
From the definition of voltage, the work
done in accumulating a small charge of dq
on the capacitor plates is given by,
`\dw=v dq" "…(8)`
From equations (7) and (8), we get,
`\dw=Cv dv" "…(9)`
Therefore, the total work done in raising
the voltage of the uncharged capacitor to source voltage V is given by,
`\W=∫_0^V Cv dv`
`\⟹W=C[v^2/2]_0^V`
`\∴W=1/2 CV^2" "…(10)`
This workdone is stored in the capacitor
in the form of an electrostatic field.
Equation (10) may also be given by,
`\W=1/2 (QV)" "[∵C=Q/V]" "…(11)`
Or,
`\W=1/2C Q^2" "[∵V=Q/C]" "…(12)`
Thus, we can calculate the energy stored
in a capacitor by using any of the equations (10), (11), or (12).
It should be noted that an ideal
capacitor does not dissipate or consume energy, but it stores only. The stored
energy is returned to the circuit during discharging of the capacitor.
Applications of Capacitors
Capacitors are used in almost all
electronic circuits. Some most common applications of capacitors are:
- Capacitors are used for energy storage in electronic circuits for a short duration.
- Capacitors are used for power conditioning to provide consistent energy levels.
- Capacitors in the form of a capacitor bank can be used for pulsed power purposes.
- Capacitors are also used for power factor correction in power systems.
- Capacitors are also used in sensors and other sensing applications.
- Capacitors are used for coupling applications because they can pass AC signals and block DC signals.
- Capacitors are also used in tuning circuits of radio systems.
- Capacitors are also used in computer memory like DRAMs.




.png)



0 Comments