A capacitor is a
passive circuit element that stores electrical energy in the form of an electrostatic
field. The ability of a capacitor to store energy in the form of electrostatic
charge is known as the capacitance
of the capacitor.
In electrical and electronic circuits, capacitors are used
to introduce a certain value of capacitance. Sometimes we do not have a single
capacitor of the desired value, in that case, we connect several capacitors either
in series or parallel or both to obtain the desired value of capacitance in the
circuit.
The capacitance of a capacitor is given by,
`\C=Q/V" "…(1)`
Where C
is the capacitance of the capacitor, Q
is the charge on the capacitor, and V
is the potential difference across the capacitor.
Series Combination of Capacitors
When several capacitors are connected end to end so that
there is only one path for electric charge (or current) to flow is called the series combination of capacitors. In
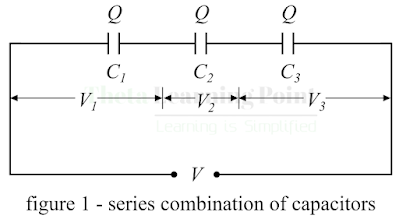
the series combination of capacitors, the electric charge on each capacitor
remains the same, but the potential difference across each capacitor is
different.
Now, let us derive the expression of equivalent capacitance when several capacitors are connected in series. For that consider three capacitors having capacitances C1, C2, and C3 respectively, connected in series across a voltage of V volts as shown in figure-1.
Here, the total voltage V
is the algebraic sum of the voltage across each capacitor, i.e.
`\V=V_1+V_2+V_3" "…(2)`
From equation (1), we have,
`\V=Q/C`
Therefore, equation (2) can be written as
`\Q/C_(eq) =Q/C_1 +Q/C_2 +Q/C_3 `
`\⟹Q/C_(eq) =Q(1/C_1 +1/C_2 +1/C_3)`
`\∴1/C_(eq) =1/C_1 +1/C_2 +1/C_3" "…(3)`
Hence, when several capacitors are connected in series, then the reciprocal of
total equivalent capacitance is equal to the sum of reciprocals of the
individual capacitances.
Special Cases:
Case
1 – When N capacitors,
each of equal capacitance (say C),
are connected in series. Then, the total capacitance of such a series
combination is given by,
`\C_(eq)=C/n" "…(4)`
Case
2 – When two capacitors of capacitances C1 and C2
respectively are connected in series. Then, their equivalent capacitance is
given by,
`\1/C_(eq) =1/C_1 +1/C_2 `
`\⟹1/C_(eq) =(C_2+C_1)/(C_1 C_2 )`
`\∴C_(eq)=(C_1 C_2)/(C_1+C_2 )" "…(5)`
Hence, the equivalent capacitance of two capacitors connected in series is
equal to the product divided by the sum of the capacitances of the two
capacitors.
Parallel Combination of Capacitors
When one end of each capacitor is
connected to a common point and the other end of each capacitor is connected to
another common point so that there are as many paths for current flow as the
number of capacitors, it is called a parallel
combination of capacitors.
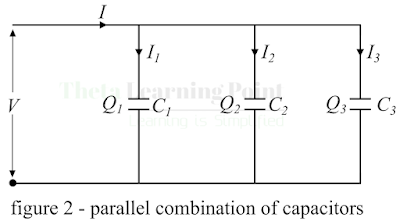
In the parallel combination of
capacitors, the voltage across each capacitor is the same, but the charge
stored on each capacitor is different.
Refer the circuit, the total current is
equal to the algebraic sum of the current through each capacitor, i.e.
`\I=I_1+I_2+I_3" "…(6)`
From the definition of electric current,
we have,
`\Q/t=Q_1/t+Q_2/t+Q_3/t`
`\⟹Q=Q_1+Q_2+Q_3" "…(7)`
Now, for a capacitor, we know,
`\Q=CV" "…(8)`
Hence, we may also write equation (7) as
follows,
`\C_(eq) V=C_1 V+C_2 V+C_3 V`
`\⟹C_(eq) V=V(C_1+C_2+C_3 )`
`\∴C_(eq)=C_1+C_2+C_3" "…(9)`
Hence, when several capacitors are connected in parallel, the equivalent
capacitance of the combination is equal to the sum of the individual
capacitances.
Special
Case:
When N
number of capacitors are connected in parallel, each capacitor has the same
capacitance (say C). Then, the
equivalent capacitance of the combination is given by,
`\C_(eq)=NC" "…(10)`
Important Point about Combinations of
Capacitors
The following are the important points about the series combination of capacitors-
- The current flowing through each capacitor is the same.
- The charge stored on each capacitor in a series combination is the same.
- The voltage across each capacitor in a series combination is different and it depends upon the value of the capacitance of the capacitor.
- The total capacitance of the series combination is less than the smallest of the capacitances.
The following are the important points about the parallel combination of capacitors-
- The current through each capacitor is different and depends upon the value of capacitance.
- The charge stored on each capacitor is different and depends upon the capacitance value.
- The voltage across each capacitor in parallel combination is the same.
- The total capacitance of the parallel combination is greater than the largest of the capacitances.
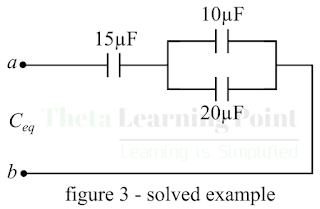
Numerical
Example – Find the equivalent capacitance of the
circuit shown in figure-3.
Step
1 – 10
µF and 20 µF are connected in parallel:
`\C^'=10+20=30" μF"`
Step 2 – C’
and 15 µF are connected in series:
`\C_(eq)=(30×15)/(30+15)`
`\∴C_(eq)=450/45=10" μF"`

.png)