In this article, we discuss the electric current, the drift velocity of electrons, current density and the relation between electric current and drift velocity, and the relation between current density and drift velocity.

Electric Current

The rate of change flow of electric charge is called electric current. The electric current is denoted by symbol ‘I (constant current)’ and ‘i (time-varying current)’. Mathematically, the electric current is given by the electric charge divided by time, i.e.

I=Qt

Where, Q is the electric charge in coulomb and t is the time in seconds. Therefore, the current is measured in coulomb per second (C/s), where,

1 C/s = 1 Ampere

Drift Velocity

The drift velocity of free electrons is defined as the average velocity with which the free electrons get drifted, i.e. moved in a metallic conductor in a specific direction under the influence of an electric field. It is denoted by v_d and is measured in meters per second.

Generally, the drift velocity of the free electrons is of the order of 10^-5 m/s. However, the drift velocity of electrons is very small, but it is entirely responsible for the flow of electric current in the metallic conductors.

Relation between Current and Drift Velocity

Consider a small portion of a metallic conductor (say copper wire) through which a current of I amperes is flowing as shown in the following figure.

Let,

l = length of the wire

A = area of cross-section of wire

Therefore, the volume (V) of the conductor wire is

V=A×l

If n is the electron density, i.e. number of free electrons per unit volume of the conductor, then,

Total number of electrons in the conductor = n × A × l

Therefore,

Total charge in the conductor, Q = n × A × l × e

Where, e is the charge on one electron and is equal to –1.6×10^-19 C.

If the electron takes t seconds to cross the conductor, then we have,

t=lvd

Where, v_d is the drift velocity of free electrons.

Now, by the definition of electric current, we have,

I=Qt

I=neAl(l/vd)

Therefore, the relation between current and drift velocity will be,

∴I=neAvd

Since, for a given conductor n, e, A are constant. Therefore,

I∝vd

i.e. the electric current flowing through a conductor is directly proportional to the drift velocity of free electrons.

Also Read :AC Power – Active, Reactive and Apparent Power

Also Read :What is Voltage Source and Current Source? – Ideal & Practical

Also Read :Ohm’s Law – Statement, Formula and Solved Examples

Current Density

The current density is defined as the current per unit area. It is denoted by the symbol J and is measured in Ampere per square meter (A/m²).

J=IA

Hence, the relation between current density and drift velocity can be established as follows,

J=neAvdA

∴J=nevd

Numerical Example – The density of conduction electrons in a copper wire is 8.5×1028 m−3. If the radius of the wire is 0.8 mm and it is carrying a current of 3 A, what will be the average drift velocity of electrons?

Solution – Given data,

n=8.5×1028 m−3

I=3 A

r=0.8 mm

Therefore, the area of cross-section (A) of the wire is

A=πr2

⟹A=π×(0.8×10−3)2

⟹A=2×10−6 m2

Now, since we know that the relation between current and drift velocity is given by,

I=neAvd

Therefore, the drift velocity of electrons is given by,

vd=IneA

⟹vd=3(8.5×1028)×(1.6×10−19)×(2×10−6)

∴vd=1.1×10−4 ms−1

Hence, in this article, we discussed about the electric current, drift velocity, and the relationship between current and drift velocity.

In this article, we will discuss the construction of DC machines (DC Motor and DC Generator). But before that let us first learn a bit about DC machines.

Introduction to DC Machine

A device that converts direct current electricity into mechanical energy or mechanical energy into direct current electricity is known as a DC Machine. Therefore, a DC machine is an electromechanical energy conversion device.

When the DC machine converts mechanical energy into dc electrical energy, it is called a dc generator. When the dc machine converts dc electrical energy into mechanical energy, it is called a dc motor.

Actually, the basic construction of a dc motor and dc generator is similar. Therefore, a dc machine can be made to operate as a dc motor and a dc generator. However, the principle of operation of the dc motor and dc generator is different.

Construction of DC Machines

A typical dc machine consists of the following major parts:

• Yoke or Frame
• Magnetic Field System
• Armature
• Commutator
• Brushes
• Bearings

The overall constructional view of a dc machine is shown in figure-1 below.

Now, let us discuss each part of the dc machine in detail.

(1). Yoke or Frame:

The yoke is the outer frame of the dc machine. The yoke or frame of the dc machine serves the following three purposes:

• The yoke protects the internal parts like the windings of the dc machine from mechanical damage.
• It provides housing for the magnetic field system.
• The yoke carries the working magnetic flux in the machine.

The yoke of a dc machine is made of a material having high permeability and high mechanical strength. Usually, the yoke of the dc machine is made up of cast steel.

Also Read :Resistors in Series and Parallel Combinations – Explanation and Examples

(2). Magnetic Field System:

The magnetic field system in a dc machine is a system of electromagnets that are excited by a dc supply. It produces the required working magnetic flux in the machine. In dc machines, the field system is a stationary part and is fixed with bolts to the yoke or frame of the machine.

In large dc machines, the magnetic field system has the following parts namely, pole core, pole shoes, and field windings.

• Pole Core: The pole core houses the field windings. The Pole core is made up of thin steel laminations. One end of the pole core is fixed to the machine frame with the help of bolts and the other end has a pole shoe.
• Pole Shoes: It is the projected part of the field pole having a large cross-sectional area. The primary function of the pole shoe is to spread the magnetic flux uniformly in the air gap. It also supports field winding.
• Field Windings: Field windings are coils made up of copper wire. Field windings are former wounds, and are inserted around the pole core. When the field windings are excited by a dc supply, they become electromagnets and produce the working magnetic flux in the air gap of the machine.

(3). Armature:

In dc machines, the armature is a rotating part (rotor). It has a system of conductors. The EMF and torque are developed in the armature of the dc machine. The Armature of a dc machine has two major parts: armature core and armature winding.

• Armature Core: The armature core is a solid cylindrical structure. The armature core usually comprises thin silicon steel laminations with high permeability. The Armature core has slots on the outer periphery to carry the armature winding.
• Armature Winding: Armature winding of a dc machine is a coil of conductor wires such as copper wires. In dc machines, depending upon the end connection of armature conductors, the armature winding can be of two types namely, Lap Winding and Wave Winding. The type of armature winding decides the voltage and current ratings of the dc machine.

Also Read :What is a Resistor – Definition, Symbol, Types, and Applications

(4). Commutator:

In dc machines, the commutator is an important part. The commutator is basically a rotating rectifier switch. It performs the following two functions:

• It collects the current from the armature conductors or allows the current to flow into the armature conductors.
• It converts the alternating current of the armature winding into a unidirectional current in the external circuit and vice-versa.

It is important to note that in a dc machine, the armature current is always alternating in nature.

The commutator of a DC machine is shown in the above figure. It is a cylindrically shaped component made up of copper. The V-shaped slots are provided on the outer periphery of the commutator to carry the commutator segments. Commutator segments are nothing but copper bars inserted in these V-shaped slots. Each commutator segment is insulated from the other by the mica material. The commutator is mounted on the rotor shaft of the dc machine on one side.

Also Read :AC Power – Active, Reactive and Apparent Power

(5). Brushes:

In dc machines, brushes are made up of carbon or graphite. Brushes are used to collect current from the rotating commutator. The carbon brushes are housed in brush holders and be in contact with the commutator surface with the help of pressure created by springs.

(6). Bearings:

In dc machines, bearings are used to reduce frictional losses. Bearings support the machine shaft. In dc machines, two types of bearings are generally used viz. ball bearing and roller bearing.

Hence, this is all about the construction of a DC machine.

In this article, we will discuss Kirchhoff’s Circuit Laws – KCL (Kirchhoff’s Current Law) and KVL (Kirchhoff’s Voltage Law). Both KCL and KVL allow us to analyze and solve complex electric circuits. Using KCL and KVL, we can determine the values of electric currents and voltages in an electric circuit. Kirchhoff’s Current Law (KCL) is the basis of the nodal analysis technique whereas Kirchhoff’s Voltage Law (KVL) is the basis of the mesh analysis technique of circuit analysis. One major advantage of KCL and KVL is that they are equally valid for both DC circuits and AC circuits.

In the year 1847, German Physicist Gustav Robert Kirchhoff introduced two laws to describe the relationship between the currents and voltages in an electric circuit. Kirchhoff’s law along with Ohm’s law forms the basis of electric circuit theory.

From the basic theory of electric circuits, we have Ohm’s law to analyze electric circuits. But, Ohm’s law by itself is not enough to analyze all kinds of circuits. Although, when Ohm’s law is coupled with Kirchhoff’s laws, we get a set of powerful tools for analyzing a wide variety of electric circuits.

Kirchhoff’s first law, i.e. Kirchhoff’s Current Law is based on the law of conservation of electric charge, which means the algebraic sum of charges within a system remains constant.

Now, let us discuss Kirchhoff’s two laws (KCL and KVL) one by one-

Kirchhoff’s Current Law (KCL)

KCL is related to the currents at the junctions (a point in an electric circuit where three or more circuit elements meet) of an electric circuit and may be stated as under-

“The algebraic sum of currents meeting at a junction in an electric circuit is zero.”

Here, the algebraic sum is one in which the sign of the quantity is taken into account.

Also Read : What is RMS Value of AC?

Explanation:

Consider five conductors carrying currents I₁, I₂, I₃, I₄, and I₅ meeting at a point O as shown in figure-1. Now, if we take the signs of electric currents entering point O as positive and the signs of electric currents leaving point O as negative. Then, according to KCL, we get,

I1+I2+(−I3)+I4+(−I5)=0

⟹I1+I2+I4=I3+I5

I.e.

Sum of incoming currents = Sum of outgoing currents

Hence, Kirchhoff’s Current Law (KCL) may also be stated as,

The sum of electric currents entering a node in an electric circuit is equal to the sum of electric currents leaving that node.

KCL is true for a node because the electric current is only the flow of electric charge, and it cannot be accumulated at any point in the circuit. This is in accordance with the law of conservation of electric charge.

Kirchhoff’s Voltage Law

Kirchhoff’s Voltage Law (KVL) is related to the EMFs and voltage drops in a closed circuit and may be stated as under-

In any closed electric circuit, the algebraic sum of all the electromotive forces and voltage drops in passive elements (ex. resistors) is equal to zero, i.e.

Algebraic sum of EMFs + Algebraic sum of the voltage drops = 0

Also Read :What are the Advantages and Disadvantages of Alternating Current?

Explanation:

Consider a closed electric circuit that is consisting of two resistors R₁ and R₂ in series connected across a source of emf E as shown in figure-2. Now, if we start from point A in this closed circuit and come back to this point A after going around the circuit. Then, there is no net change in the potential. This means the algebraic sum of EMFs of all the energy sources in the path plus the algebraic sum of the voltage drops in the passive elements must be zero.

In the given closed circuit, when we apply KVL, we get,

E+(−IR1)+(−IR2)=0

⟹E=IR1+IR2

The KVL is based on the law of conservation of energy. That means the net change in the energy of an electric charge after completing the closed path in an electric circuit is zero.

Also Read : What is Voltage?

Sign Convention:

While applying KVL in a closed electric circuit, we deal with the algebraic sum of EMFs and voltage drops in the circuit. Therefore, it is important to use a proper sign of EMFs and voltage drops in the closed circuit. In actual practice, the following sign convention is followed:

A rise in potential across an element of the circuit is considered positive and a drop in the potential across an element of the circuit is considered negative.

Numerical Example (1) – Determine the electric current flowing through the 5 Ω resistor in the circuit shown in figure-3.

Solution – Applying Kirchhoff’s Current Law at node (a), we get,

Sum of incoming current = Sum of outgoing currents

15+10=I

∴I=25 A

Hence, the current through 5 Ω resistor is equal to 25 A.

Numerical Example (2) – Determine the voltage drop across the 5 Ω resistor in the circuit shown in figure-4.

Solution – Applying Kirchhoff’s Voltage Law in the closed loop, we can write,

Sum of EMFs = Sum of Voltage Drops

14=4+V

V=10 V

Hence, the voltage drop across the 5Ω resistor in the circuit is 10 Volts.

Conclusion

We may conclude the above discussion with the following points:

• Kirchhoff’s Current Law (KCL) states that in any electric circuit, the algebraic sum of currents entering a node is equal to the algebraic sum of leaving current at that node.
• KCL is based on the law of conservation of electric charge.
• KCL is also known junction rule of circuit analysis.
• Kirchhoff’s Voltage Law (KVL) states that in any closed electric circuit, the algebraic sum of all the EMFs equals the algebraic sum of all the voltage drops.
• KVL is based on the law of conservation of energy.
• KVL is also known as the loop rule or mesh rule of circuit analysis.

Related Articles

• Ohm’s Law
• Nodal Analysis
• What is Electric Current?

In this article, we will discuss the basic terms related to AC (Alternating Current) circuits.

Knowledge of this terminology is very important to study AC circuits. Hence, every electrical engineering student and professional must know the meaning of these basic terms of AC circuits.

In the upcoming sections of this article, we will discuss the following six major terms related to ac circuits:

• Waveform
• Cycle
• Time Period
• Frequency
• Phase Angle
• Phase Difference

Now, let us discuss these terms of AC circuits in detail one by one.

(1). Waveform:

The curve or graph obtained by plotting instantaneous values of an AC quantity (current or voltage) against time is called the waveform of the AC quantity.

Consider a sinusoidally varying alternating voltage expressed by,

v=Vm sinωt

The waveform of this alternating voltage is shown in figure-1 below.

(2). Cycle:

One complete set of positive and negative instantaneous values of an alternating wave is called a cycle. In other words, one complete set of alterations is called the cycle of the ac wave. One complete cycle of the alternating voltage (v) is shown in figure-1 above.

Here, in one complete cycle, there are two half cycles, i.e. one positive half cycle and one negative half cycle.

(3). Time Period:

The time taken to complete one cycle by the AC wave is called its time period. The time period is usually denoted by T.

For the AC wave shown in figure-1, the time period is equal to 2π. In other words, for a sinusoidal ac wave, during one time period T, the change in the angle of the wave is equal to 2π. Therefore,

θ=ωT=2π

∴T=2πω

The time period is measured in seconds (s).

(4). Frequency:

The number of cycles completed by the AC wave in one second is called the frequency of the AC wave. Frequency is denoted by “f”.

The ac wave shown in figure-1, one cycle is completed in T seconds. Therefore, in 1-second 1/T cycles will be completed. Hence, the frequency is given by,

f=1T

Frequency is measured in cycles per second (c/s). The SI unit of frequency is Hertz (Hz).

Since, we have,

T=2πω

Therefore, the frequency can also be given by,

f=ω2π

Thus, the relationship between angular frequency (ω) and linear frequency (f) is given by,

ω=2πf

Where the angular frequency ω is measured in radians per second.

(5). Phase Angle:

The angle of an AC wave at t = 0 is called the phase angle of the AC wave. For example, consider an ac wave expressed by the following expression,

i=Im sin(ωt+ϕ)

At any instant of time (t), the angle of the wave is equal to (ωt + ϕ). But at t = 0, we have, the angle of the wave equal to ϕ. Therefore, ϕ is called its phase angle.

(6). Phase Difference:

The angular separation between the zero crossing points of two ac waves is called the phase difference between them.

Let us consider three sinusoidal current waves of the same magnitude,

i1=Im sinωt

i2=Im sin(ωt+θ1)

i3=Im sin(ωt−θ2)

The waveform representation of these currents is shown in the figure-2 below.

Here, it can be seen that the current i₁ starts at t = 0, thus, it may be taken as the reference wave.

By definition, the angular distance between zero crossing points of two waves is called phase difference. Thus, the angle θ₁ is the phase difference between i₁ and i₂, and θ₂ is the phase difference between i₁ and i₃.

The phase difference between two ac waves can be numerically computed by finding the difference in the phase angles of the two waves.

For example, from the figure-2, we have,

Phase difference between i₂ and i₁ = Δθ = θ₁ – 0

⇒Δθ=θ1

In general,

Δθ=θ

• If Δθ is positive, then i₂ is said to be leading the current wave i₁ by an angle of Δθ.
• If Δθ is negative, then i₂ is said to be lagging the current wave i₁ by an angle of Δθ.

Hence, in figure-2, we can conclude,

• The wave i₂ leads i₁ by an angle θ₁.
• The wave i₃ lags i₁ by an angle θ₂.
• The wave i₂ leads i₃ by an angle (θ₁ + θ₂).
• The wave i₃ lags i₂ by an angle (θ₁ + θ₂).

In general, if the phase angle of an AC wave is θ, it is said to be leading from the reference wave. On the other hand, if the phase angle of an AC wave is –θ, it is said to be lagging from the reference wave.

Therefore, this is all about the six most important terms associated with AC circuits in electrical engineering.

In this article, we shall discuss Resistor, their definition, circuit symbol, types, and applications in various electrical and electronic circuits.

What is a Resistor?

A passive circuit element that is used to introduce electrical resistance in an electrical or electronic circuit is called a Resistor. It is a passive circuit component as it only consumes electrical energy, and does not deliver electrical energy. The measurement of opposition that a resistor offers in the flow of current through it, is called resistance. The resistance is represented by the symbol R.

The resistor is a circuit element used to model the current-resisting behaviour of a material. We may also define the resistor in terms relation between voltage and current as, a circuit element for which the voltage across the element is directly proportional to the current through it, then the element is called a resistor.

Working of Resistor

In a resistor, electrons moving under the influence of an electric field collide with positive atoms of the resistor material again and again. After each collision, these electrons slow down and the number of electrons crossing per unit area is reduced. Consequently, the current through it is reduced, and the energy released on each collision is dissipated in the form of heat. In this way, a resistor opposes the flow of electric current.

Types of Resistors

The resistors can be of the following two types, namely-

• Fixed Resistors
• Variable Resistors

(1). Fixed Resistor:

A resistor whose resistance remains constant is called a fixed resistor. It is the most widely used type of resistor. These are mainly used in electronic circuits to introduce a constant resistance in a circuit. The resistance value of fixed resistors is determined during their manufacturing, and these resistors come in standard resistance values. The circuit symbol of the fixed resistor is shown in figure-1.

There are several types of fixed resistors available such as carbon composition resistors, carbon film resistors, metal-oxide film resistors, metal film resistors, wire wound resistors, surface mount resistors, etc.

Also Read : What is Mesh Analysis?

(2). Variable Resistor:

A resistor whose resistance value can be adjusted as per requirement is called a variable resistor. A variable resistor consists of two main parts viz. an element of fixed resistance and a slider. The slider taps onto the fixed resistor element. Therefore, a variable resistor has three connection terminals – the two terminals are of the fixed resistor element and the third is the slider terminal. When we are required to provide a resistor with variable resistance, one end of the fixed resistor element and the slider terminal are connected in the circuit. The circuit symbol of the variable resistor is shown in the figure-1.

The variable resistors can also be of either wire-wound or composition type. A most commonly used variable resistor, called a potentiometer or pot, is a three-terminal element with a slider. By sliding the slider, the resistance between the slider terminal and the fixed terminals can be adjusted.

Depending upon Ohm’s law, resistors may also be classified into two types, namely-

Also Read :What are Smart Grid Drivers?

(1). Linear Resistor –

A resistor that obeys Ohm’s law is known as a linear resistor. A linear resistor always has a constant resistance and hence its current-voltage characteristic is a straight line passing through the origin as shown in figure-2.

Also Read :Electrolysis – Definition, Facts, and Applications

(2). Non-Linear Resistor –

A resistor that does not obey ohm’s law is known as a non-linear resistor. The resistance of a non-linear resistor varies with the current through it. Therefore, the current-voltage characteristic of the non-linear resistors is not a straight line, i.e. it has a different slope at different points. The figure-3 shows a current-voltage characteristic of a typical non-linear resistor. Examples of devices with non-linear resistive behaviour are the electric light bulb and the diode.

Although, all practical resistors may exhibit non-linear resistive behaviour under certain conditions.

Applications of Resistors

The resistor is one of the fundamental components in electrical and electronic circuits. The primary use of the resistor is to control the flow of electric current in a circuit. The following are some major applications of resistors-

• Resistors are used in different circuit functions like speed control of a motor, changing the loudness of an amplifier, etc.
• Resistors are used for designing voltage divider circuits.
• Resistors are used in electric heating appliances as the current passing through a resistor generates heat.
• Resistors are used in light-dimming circuits.
• Resistors are also used in fan regulators, etc.

Conclusion

In this article, we discussed resistors, their types, and their applications. From the above discussion, it is clear that a resistor is a two-terminal passive circuit element that is used in various electrical and electronic circuits to introduce a certain amount of electrical resistance. The main use of a resistor in a circuit is to control the current through it.

In this article, we will discuss the form factor and peak factor. Both form factor and peak factor are two important measures related to alternating quantities. The form factor is used for describing the distortion and heating effect of an alternating signal. While, the peak factor is used to get information about the maximum value of the alternating quantity, and thus helps in differentiating the two waveforms.

What is a Form Factor?

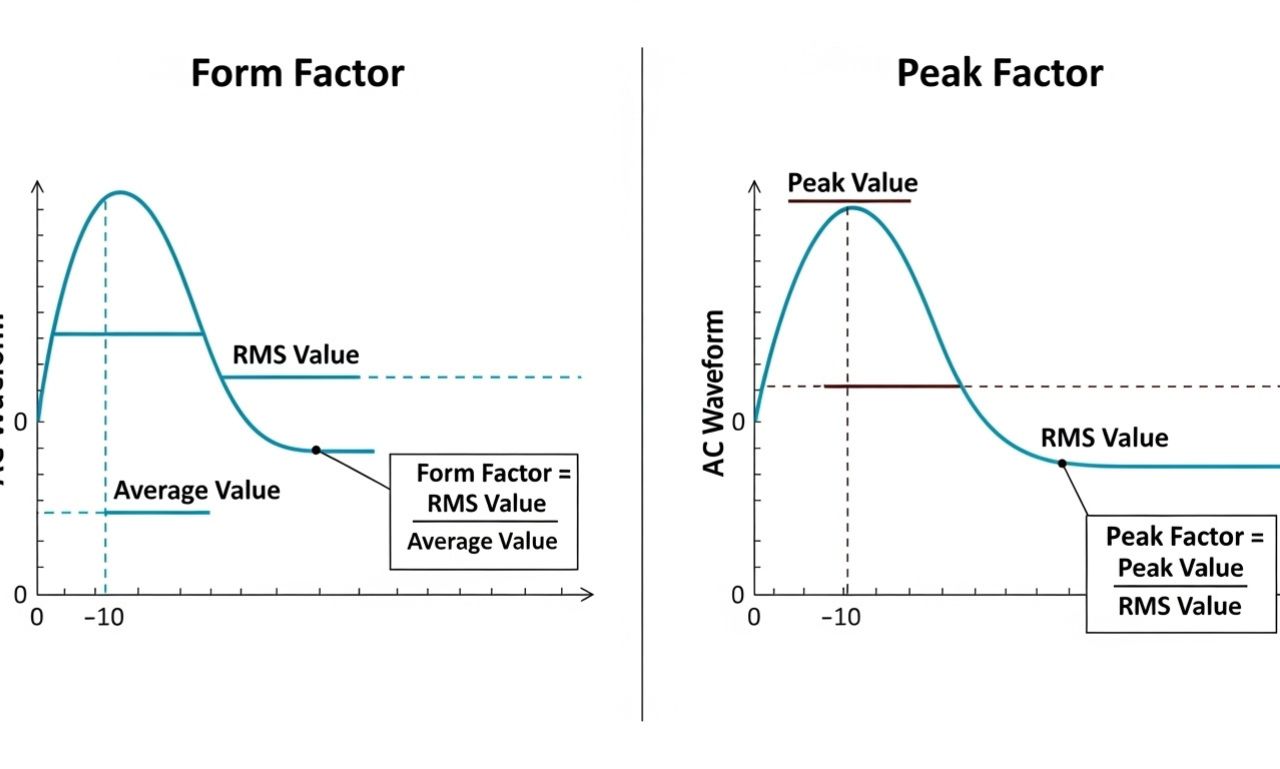
In electrical engineering, the waveforms of two different alternating quantities of the same maximum or peak values and the same frequency may look different, which means there could be a difference in their configuration. This difference in the configuration of periodic waveforms where the amplitudes and frequencies are the same is represented by the form factor (FF).

For an alternating quantity such as alternating current or voltage, the form factor is defined as the ratio of the RMS (Root Mean Square) value to the average value of the alternating quantity. Therefore,

Form Factor=RMS ValueAverage Value

For alternating current, the form factor is expressed as,

Form Factor=IRMSIav

For alternating voltage, the form factor is expressed as,

Form Factor=VRMSVav

The form factor formulae and values of different types of alternating quantities are given as follows-

(1). The form factor of a sinusoidal (sine) wave is:

Form factor=(π/2)√2=1.11

(2). The form factor of a half-wave rectified sine wave is:

Form factor=π2=1.57

(3). The form factor of a full-wave rectified sine wave is:

Form factor=(π/2)√2=1.11

(4). The form factor of a square wave is:

Form Factor = 1

(5). The form factor of a triangular wave is:

Form factor=2√3=1.155

(6). The form factor of a saw-tooth wave is:

Form factor=2√3=1.155

What is a Peak Factor?

The peak factor gives an idea about the maximum value of an alternating quantity (current or voltage) that its waveform can provide. The peak factor also helps in deriving the waveform of a signal from the DC signal.

The peak factor of an alternating quantity may be defined as under-

The ratio of the maximum or peak value to the RMS value of an alternating quantity is known as the peak factor of the alternating quantity. It is also known as the crest factor because the peak value is also called the crest value.

Mathematical, the peak factor or crest factor can be expressed as,

Peak factor=Peak valueRMS value

For an alternating current, the peak factor is given by,

Peak factor=ImIrms

For an alternating voltage, the peak factor is given by,

Peak factor=VmVrms

Where I_m and V_m are the maximum or peak values of the current and voltage respectively, and I_rms and V_rms are the root mean square (RMS) values of the current and voltage respectively.

The peak factor of a sinusoidal alternating current is:

Peak factor=Im(Im/√2)=√2=1.414

The peak factor of a sinusoidal alternating voltage is:

Peak factor=Vm(Vm/√2)=√2=1.414

Numerical Example – The RMS value of a sinusoidal voltage is 141.4 V and the average value is 127.4 V. If the maximum value of the given voltage is 200 V. Then, determine the form factor and peak factor of the voltage waveform.

Solution – Given data,

VRMS=141.4V

Vav=127.4V

Vm=200V

Therefore, the Form factor of the given voltage waveform is:

FF=VRMSVav

⟹FF=141.4127.4=1.11

The peak factor of the voltage waveform is:

PF=VmVrms

⟹PF=200141.4=1.414

Hence, for the given sinusoidal voltage wave, the form factor is 1.11 and the peak factor is 1.414.

Conclusion

Thus, in the above sections of this article, we discussed what the form factor and peak factor are. The form factor is related to the RMS value and average value of the alternating quantity, and the peak factor is related to the peak and RMS values of the alternating quantity.

Related Articles

• Electric Circuit – Definition and Types
• Electric Current – Definition, Formula, Unit, and Types
• Ohm’s Law – Statement, Proof, and Examples
• Electrical Power and Electrical Energy
• Electric Potential and Voltage